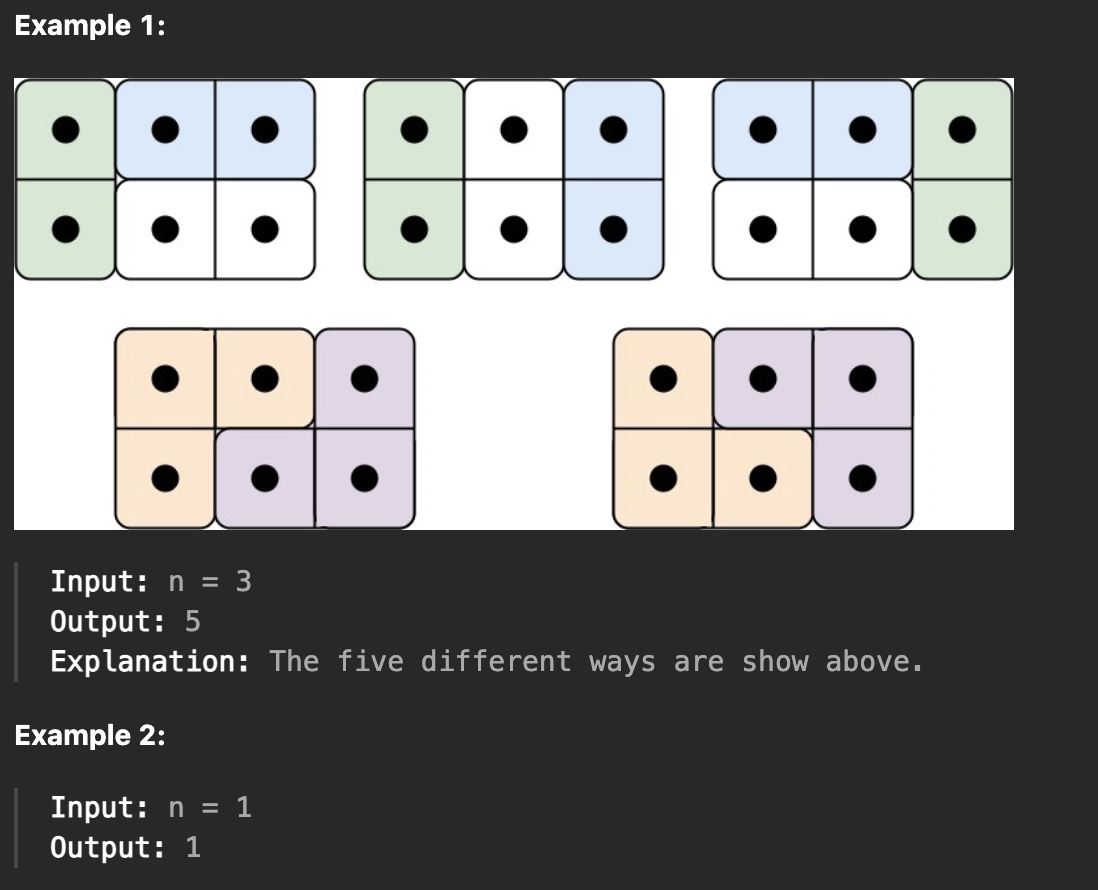
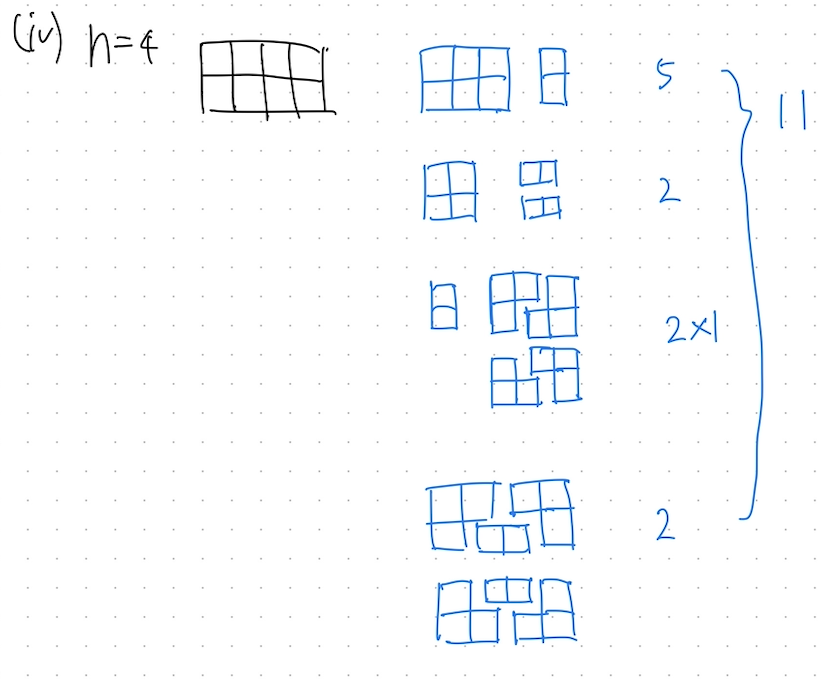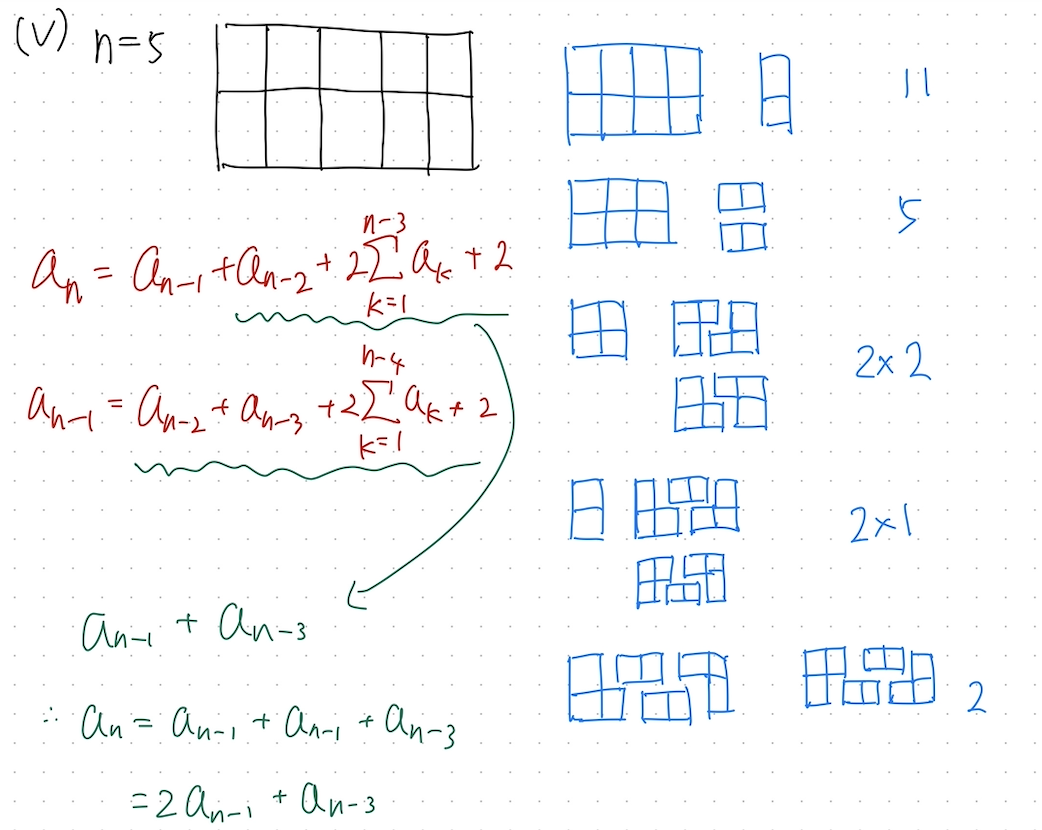题目概述
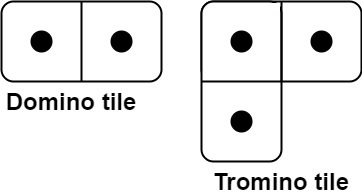
You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.
Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 10^9 + 7.
In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.
Constraints:
1 <= n <= 1000
思路
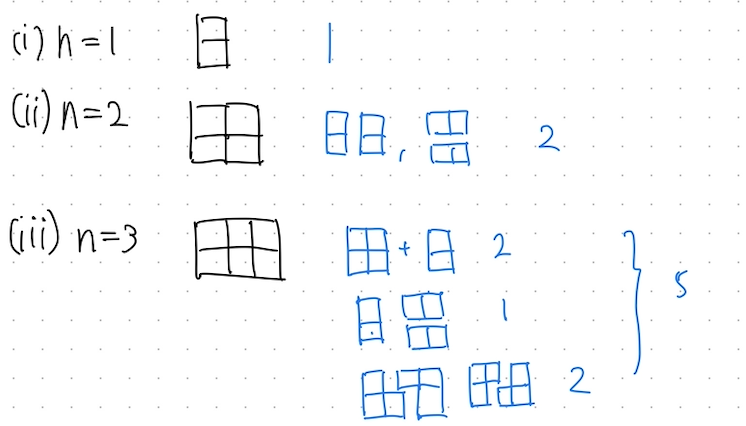
乍一看这题有些摸不着头脑,总之先归纳一下n在1~3这个范围内时铺瓷砖的情况。
n = 3时,可以分为三种情况去统计可能的铺瓷砖方式:
- 将瓷砖分为
2 x 2和2 x 1的左右两部分,此时左半边根据n = 2的结果可以得知有两种铺法 - 将瓷砖分为
2 x 1和2 x 2的左右两部分,其中右半部分按照横向的1 x 2形状进行分割(否则会和前一种情况重复) - 最后是不利用之前结果的铺法,也就是
n = 3时的特有铺法
我们可以再看一下n = 4和n = 5时的情况
还是采用类似的思考方式,这时可以发现规律了。若令$a_n$表示地面为2 x n时可能的铺瓷砖方式总数,那么有:
或者可以简化成:
\[a_n = \begin{cases} 1 \qquad&, n = 0\\ 1 &, n = 1\\ 2 &, n = 2\\ a_{n - 1} + a_{n - 2} + 2 \sum_{k = 0}^{n - 3} a_k &, n \geq 3 \\ \end{cases}\]那么这其实是一道动态规划的题目,只不过想要准确地找出状态转移方程还是有点难度。不过,到这一步为止感觉还是不够,因为求解的话还需要对之前所有的情况进行求和,太麻烦了。所以再考察一下相邻项之间是否存在一些联系。
\[a_{n - 1} = a_{n - 2} + a_{n - 3} + 2 \sum_{k = 0}^{n - 4} a_k \qquad, n \geq 4\]等式两边同时加上 $a_{n - 3}$, 可得:
\[a_{n - 1} + a_{n - 3} = a_{n - 2} + 2 \sum_{k = 0}^{n - 3} a_k\]于是有,
\[\begin{aligned} a_n &= a_{n - 1} + a_{n - 1} + a_{n - 3} \\ &= 2 a_{n - 1} + a_{n - 3} \end{aligned}\]这便是最终的状态转移方程了。最后看一下代码实现。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
def numTilings(self, n: int) -> int:
if n < 3:
return n
else:
dp = [0] * (n + 1)
dp[0], dp[1], dp[2] = 1, 1, 2
for i in range(3, n+1):
dp[i] = 2 * dp[i-1] + dp[i-3]
return dp[-1] % (10 ** 9 + 7)
顺利通过。