Leetcode 74 二维矩阵搜索

题目概述

Leetcode 74

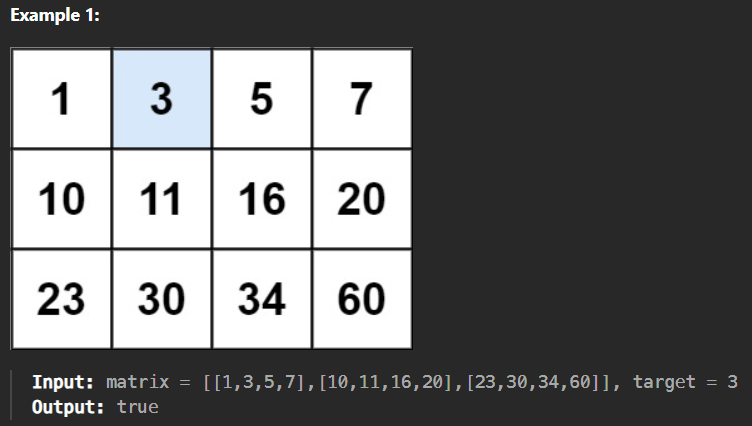
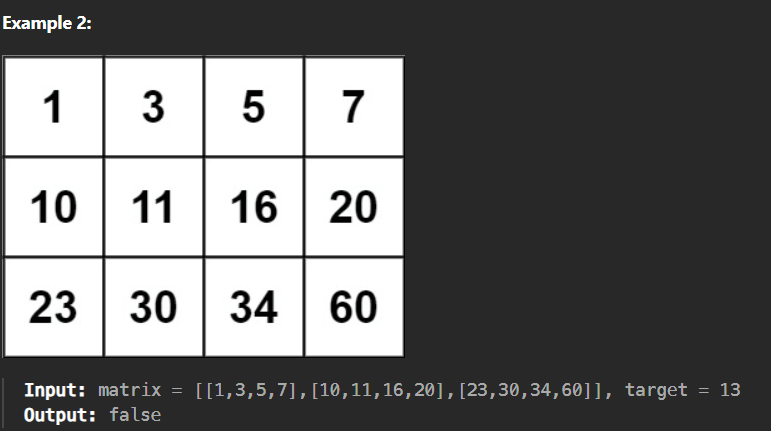
You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10^4 <= matrix[i][j], target <= 10^4

思路

题目要求我们在一个二维数组里查找对应的数字，并且这个矩阵中的元素已经按照由小到大的顺序事先进行了排序（行中从左到右，行间从上到下），故可以使用二分查找的方法。

代码实现

最初的思路是依次对target可能存在的行与列进行二分查找，因此需要四个变量分别表示行与列最初的查找范围，也就是下面代码中的row_left, row_right, column_left, column_right。随后便进入二分查找的标准流程，具体代码如下：

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        row_left, row_right = 0, len(matrix) - 1
        column_left, column_right = 0, len(matrix[0]) - 1

        while row_left < row_right:
            row_mid = (row_left + row_right) // 2
            if target < matrix[row_mid][0]:
                row_right = row_mid - 1
            elif target <= matrix[row_mid][column_right]:
                row_left = row_mid
                break
            else:
                row_left = row_mid + 1

        row_id = row_left
        while column_left < column_right:
            column_mid = (column_left + column_right) // 2
            if target == matrix[row_id][column_mid]:
                return True
            elif target < matrix[row_id][column_mid]:
                column_right = column_mid - 1
            else:
                column_left = column_mid + 1

        column_id = column_left
        return matrix[row_id][column_id] == target

顺利通过。

浏览他人解法后发现其实这样写代码过于冗余了，细节部分处理得也不够到位。比如最后一步return的话其实希望直接写为return False，将判定都集中在while循环中完成。这个可以通过将while循环的终止条件修改为left <= right来实现。此外，最受启发的还是行与列索引的表示方法：如果将二维数组扁平化，也就是将每一行从左到右拼接成一个一维数组，那么对于这个数组中任意的一个元素的索引 $i$ ,可以有：

row = i // len(matrix[0])
column = i % len(matrix[0])

这样代码可以简化许多。优化过后代码如下：

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        l, r = 0, len(matrix) * len(matrix[0]) - 1

        while l <= r:
            mid = (l + r) // 2
            row, column = mid // len(matrix[0]), mid % len(matrix[0])
            
            if target == matrix[row][column]:
                return True
            elif target > matrix[row][column]:
                l = mid + 1
            else:
                r = mid - 1

        return False