Leetcode 72 编辑距离

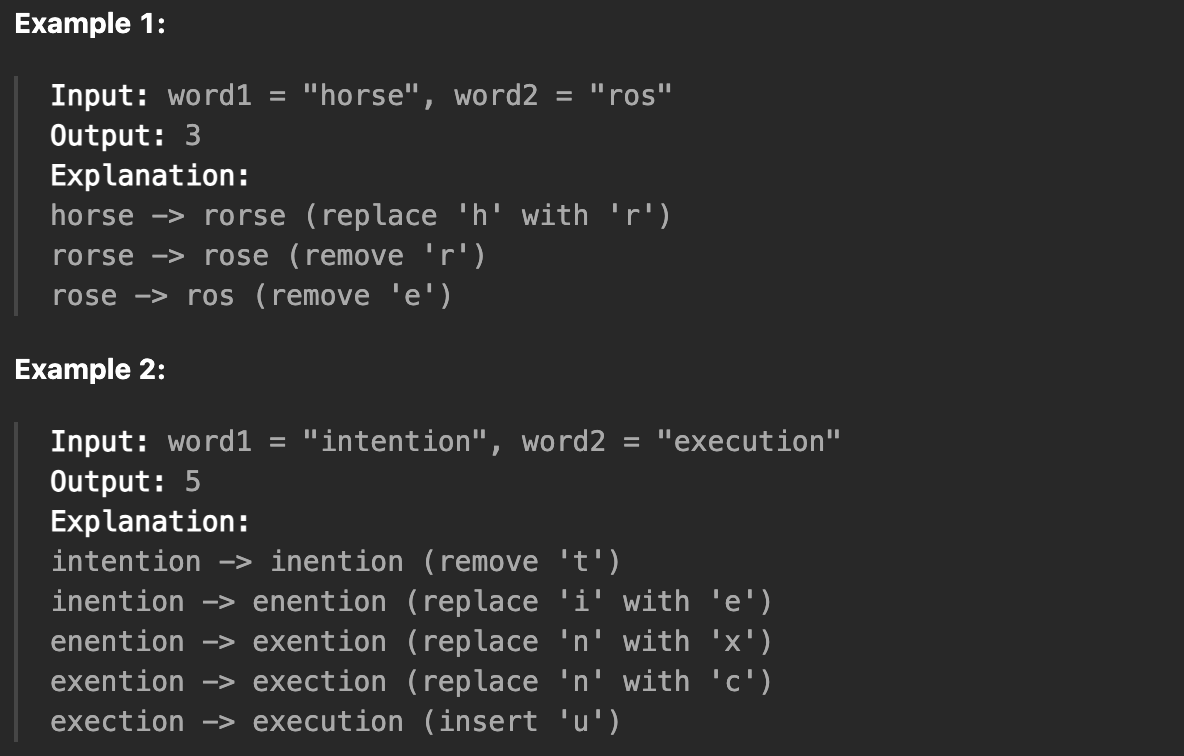
题目概述

Leetcode 72

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

• Insert a character
• Delete a character
• Replace a character

Constraints:

• 0 <= word1.length, word2.length <= 500
• word1 and word2 consist of lowercase English letters.

初步尝试

根据题意，我们需要对word1这个字符串用尽可能少的操作（添加、删除或替换字符）数（也即编辑距离），使之与字符串word2匹配。可以设想到当两个字符串相当长时，直接求解会十分困难，由此自然地会去思考能否把这个问题分解成多个子问题，此时已经预感到这道题或许可以使用动态规划来解决。那么既然要使用动态规划的话，我们需要定义一个合适的状态，也就是子问题的形态。

不妨这样设：dp[i][j]表示word1中索引值 $[0, i]$, word2中索引值 $[0, j]$ 的这两个子串所对应的编辑距离。（注意是闭区间）

接下来思考状态间是如何转移的。我们举一个例子来具体地观察一下，假设两个字符串如下所示：

\[\begin{aligned} i \quad n \quad t \quad e \quad n \quad t \quad i \quad o \quad n \\ e \quad x \quad e \quad c \quad u \quad t \quad i \quad o \quad n \end{aligned}\]

在这里有一个问题需要明确： 是否需要对不同相对位置的 $i$ 与 $j$ 进行分类讨论？在最初的思考过程中我并没有一下子弄清楚这个问题，所以不妨先实际操作一下试试看。

• 令 $i = 5$，$j = 5$：

  \[\begin{aligned} {\color{royalblue}{i \quad n \quad t \quad e \quad n}} \quad {\color{red}{t}} \quad i \quad o \quad n \\ {\color{royalblue}{e \quad x \quad e \quad c \quad u}} \quad {\color{red}{t}} \quad i \quad o \quad n \end{aligned}\]

此时两个子串的最后一位相同，无需进行额外的操作。那么这两个子串的编辑距离与各自除去最后一位的子串的编辑距离相等，即dp[i][j] = dp[i-1][j-1]

• 令 $i = 4$，$j = 4$：

  \[\begin{aligned} {\color{royalblue}{i \quad n \quad t \quad e}} \quad {\color{red}{n}} \quad t \quad i \quad o \quad n \\ {\color{royalblue}{e \quad x \quad e \quad c}} \quad {\color{red}{u}} \quad t \quad i \quad o \quad n \end{aligned}\]

此时两个子串的最后一位不同，那么就需要考虑进行三种操作后的结果是什么。

• 替换： 将最后一位替换成一样的字符之后，情况就与上文中第一种相同了，答案取决于最后一位之前的子串的编辑距离，所以结果为: dp[i][j] = 1 + dp[i-1][j-1]

• 删除： 将最后一位删除的话，则需要匹配的子串变为下方所示的蓝色部分，所以结果为：dp[i][j] = 1 + dp[i-1][j]

  \[\begin{aligned} & {\color{royalblue}{i \quad n \quad t \quad e}} \quad {\color{red}{\bcancel{n}}} \quad t \quad i \quad o \quad n \\ & {\color{royalblue}{e \quad x \quad e \quad c \quad u}} \quad t \quad i \quad o \quad n \end{aligned}\]

• 添加： 添加一个字符。首先为了使编辑距离最短，这里添加的字符一定是与word2[j]匹配的。其次得注意添加的位置有两种选择，一种是添加到word1[i]的左边，另一种则是添加到word1[i]的右边。此时需要考虑遍历字符串的顺序，word[i]的下一位是word[i+1]，而如果将新字符添加到左边会导致word[i]在并没有被匹配的情况下就被略过了。过程如下：

  \[\begin{aligned} & {\color{royalblue}{i \quad n \quad t \quad e \quad u}} \quad {\color{green}{n}} \quad {\color{red}{t}} \quad i \quad o \quad n \\ & {\color{royalblue}{e \quad x \quad e \quad c \quad u}} \quad {\color{red}{t}} \quad i \quad o \quad n \end{aligned}\]

  故添加到左边不可行。如果是添加到右边，情况如下：

  \[\begin{aligned} & {\color{royalblue}{i \quad n \quad t \quad e \quad n}} \quad {\color{red}{u}} \quad t \quad i \quad o \quad n \\ & {\color{royalblue}{e \quad x \quad e \quad c}} \quad {\color{red}{u}} \quad t \quad i \quad o \quad n \end{aligned}\]

  可以看到子串末尾已被匹配，而编辑距离取决于上方的蓝色部分。结果为：dp[i][j] = 1 + dp[i][j-1]

那么回到一开始提出的问题：是否需要对不同相对位置的 $i$ 与 $j$ 进行分类讨论？

答案是不用的。 从上述的几种状态中其实可以发现无论两个子串结尾的索引位置是否相同，我们都可以使用同样的思考方式来求解编辑距离，也就是说这些子结构之间都是等效的。否则上述的推导式从一开始就将不成立，因为那样的话状态就只有在 $i = j$ 的时候才能被定义。

至此，三种操作方式对应的状态转移方程就都推导出来了，而对于状态dp[i][j]，最终的结果应该取三种操作中编辑距离的最小值。用代码总结如下：

if word1[i] == word2[j]:
    dp[i][j] = dp[i-1][j-1]
else:
    # min(replace, delete, insert)
    dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])

但问题到这里并未被最终解决，因为可以观察到状态转移方程中有i-1, j-1的存在，故索引值中存在0的情况还需单独讨论：

• 均为0： 这时编辑距离取决于两个字符串的第一个字符是否相同，若相同则dp[0][0]为0，反之则为1。

• 有一个为0：两者等效，这里就考虑 $j = 0$ 的情况:

  \[\begin{aligned} & a \quad {\color{red}{b}} \qquad \qquad \qquad a \quad {\color{red}{b}} \\ & {\color{red}{b}} \qquad \qquad \qquad \quad \;\,\, {\color{red}{c}} \end{aligned}\]

  情况也分为子串末尾相同与不同两种。相同时dp[i][j] = dp[i-1][j], 不同时dp[i][j] = 1 + dp[i-1][j]

此外，注意到限定条件0 <= word1.length, word2.length <= 500，两个字符串的长度可以为0，也就是空字符串，所以对这种情况进行一个特判。

m, n = len(word1), len(word2)
if not word1 or not word2:
    return max(m, n)

所以边界情况的代码总结如下：

if not word1 or not word2:
    return max(m, n)
if not i and not j:
    dp[i][j] = int(word1[i] != word2[j])
elif not i:
    if word1[i] == word2[j]:
        dp[i][j] = dp[i][j-1]
    else:
        dp[i][j] = 1 + dp[i][j-1]
elif not j:
    if word1[i] == word2[j]:
        dp[i][j] = dp[i-1][j]
    else:
        dp[i][j] = 1 + dp[i-1][j]

最终提交完整代码如下：

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        m, n = len(word1), len(word2)
        if not word1 or not word2:
            return max(m, n)

        dp = [[0] * n for _ in range(m)]

        for i in range(m):
            for j in range(n):
                if not i and not j:
                    dp[i][j] = int(word1[i] != word2[j])
                elif not i:
                    if word1[i] == word2[j]:
                        dp[i][j] = dp[i][j-1]
                    else:
                        dp[i][j] = 1 + dp[i][j-1]
                elif not j:
                    if word1[i] == word2[j]:
                        dp[i][j] = dp[i-1][j]
                    else:
                        dp[i][j] = 1 + dp[i-1][j]
                else:
                    if word1[i] == word2[j]:
                        dp[i][j] = dp[i-1][j-1]
                    else:
                        # min(replace, delete, insert)
                        dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])

        return dp[-1][-1]

错误原因分析

提交结果：Wrong Answer!

给出的反例是

"pneumonoultramicroscopicsilicovolcanoconiosis"
"cltramicroscopically"

这两个字符串未免也太长了。。。那问题到底出在哪里呢？经过不断对这两个字符串进行删减的尝试后，将问题定位在了如下部分：

"pneumonou"
"u"

看起来是边界情况的状态转移出现了问题，仔细观察后发现问题出在这里：

\[\begin{aligned} & p \quad n \quad e \quad {\color{red}{u}} \quad m \quad o \quad n \quad o \quad {\color{red}{u}} \\ & {\color{red}{u}} \end{aligned}\]

结合之前状态转移的代码部分：

elif not j:
    if word1[i] == word2[j]:
        dp[i][j] = dp[i-1][j]

可以发现如果执行这段代码的话，word1中每出现一个与word2相同的字符就会跳过计算编辑距离的过程，而直接采用再往前一个子串的编辑距离。问题是出在dp[i][j] = dp[i-1][j]上。回想非边界情况时，两个子串的最后一位字符如果相同，采用的状态转移方程应当是dp[i][j] = dp[i-1][j-1]，怎么到了边界情况就变了呢？还是说从一开始我对所谓”边界情况”的判断就有误？

重新审视一遍这个问题后，我找到了答案。正如刚才所说，我对边界情况的判断出现了偏差。真正的边界情况应当是字串至少有一个为空时。这时另一个问题又出现了，该怎么定义空字符串的状态呢？因为就算是最小的索引值0也定义了子串长度为1时的情况。

再次尝试

经过一番思考后，我发现可以这么做：重新定义状态dp[i][j]为word1[:i], word2[:j]这两个子串的编辑距离。这样的话空字符串就可以用切片[:0]来表示了。而由于我们将状态定义成了切片，也就是左闭右开的形式，所以dp数组的长度需要从原来的n变成n+1。在此基础上，根据这个新的定义我们可以重新写出边界情况：

m, n = len(word1), len(word2)
dp = [[0] * (n+1) for _ in range(m+1)]

for i in range(m+1):
    dp[i][0] = i

for j in range(n+1):
    dp[0][j] = j

除此之外的部分基本不需要改变，唯独需要注意此时的i, j表示的含义已经发生转变，由原本的索引值转变成索引切片的右侧端点。所以涉及到word1, word2中的字符比较时需要将i, j转变为i-1, j-1。最后看一下代码实现。

代码实现

Time complexity: O(mn)

Space complexity: O(mn)

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        m, n = len(word1), len(word2)
        dp = [[0] * (n+1) for _ in range(m+1)]

        for i in range(m+1):
            dp[i][0] = i
            
        for j in range(n+1):
            dp[0][j] = j

        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])

        return dp[-1][-1]

顺利通过。