题目概述
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.
Constraints:
n == height.length1 <= n <= 2 * 10 ^ 40 <= height[i] <= 10 ^ 5
思路 & 代码实现
这个问题的最优解是使用双指针,想直接阅读该解法的读者朋友可以直接跳转到 这里。
解法一:Brute Force
首先,我们观察例一的图可以发现,如果一个区域能够积水,那么它必然是一个“凹”字形结构。换句话说,它必然是一个中间低、两边高的结构,也就是说它的左右各会有一个边界,并且积水的高度取决于两个边界中更低的那一个。对于于每一个点位的积水量,存在以下两种情况:
- 能够积水: 在这个点位的两边各有一个高于当前点位的边界,积水量为两个边界中高度的最小值与当前点位的高度差
- 不能够积水: 在这个点位的至少一边不存在更高的边界,因为这样便无法留住比当前高度更高的水。
转换成编程语言,对于height中每一个点位i,寻找其两侧(包含当前点位)是否存在更高的边界,左侧的最高点记为left_max,右侧的最高点记为right_max,那么每一个点位的积水量为:min(left_max, right_max) - height[i]。将所有点位的积水量相加即可求得最终的答案。
注: 无法积水的情况对应了上文中提到的至少有一侧不存在比当前点位更高的边界,因此min(left_max, right_max)的值即为height[i],所以积水量为0,符合要求。
具体代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
ans = 0
for i in range(n):
left_max, right_max = 0, 0
# 求当前点位右侧的最高边界
for j in range(i, n):
right_max = max(right_max, height[j])
# 求当前点位左侧的最高边界
for j in range(i, -1, -1):
left_max = max(left_max, height[j])
# 计算当前点位可以积的雨水量
ans += min(left_max, right_max) - height[i]
return ans
Time complexity: $O(n ^ 2)$
Space complexity: $O(1)$
暴力解法时间复杂度高,会导致TLE,无法提交通过。
解法二:动态规划
暴力解法中对于每一个点位都通过遍历height计算了两侧的最大高度。事实上这其中包含了大量的重复计算,我们可以用两个数组left_max,right_max分别用于存储对应点位的左右侧最大高度。更具体一点:
left_max[i]:代表height[i]及其左侧的最大高度。- 计算方式:
left_max[i] = max(left_max[i-1], height[i]) - 原理:当前点位及其左侧的最大高度为当前点位的高度与前一个点位及其左侧的最大高度中更大的那一个。
left_max[0]初始化为height[0]
- 计算方式:
right_max[i]:代表height[i]及其右侧的最大高度。- 计算方式:
right_max[i] = max(right_max[i+1], height[i]) - 原理:同上
right_max[-1]初始化为height[-1]
- 计算方式:
这样的话,之后只需要再对height做一次遍历,并计算每一个点位可以积的雨水量便可以得到正确答案。代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
left_max, right_max = [0] * n, [0] * n
left_max[0], right_max[-1] = height[0], height[-1]
for i in range(1, n):
left_max[i] = max(height[i], left_max[i-1])
for i in range(n-2, -1, -1):
right_max[i] = max(height[i], right_max[i+1])
ans = 0
for i in range(n):
ans += min(left_max[i], right_max[i]) - height[i]
return ans
结果顺利通过。
Time complexity: $O(n)$
Space complexity: $O(n)$
解法三:单调栈
解法二中对height进行了三次遍历,那么有没有可以只用一次遍历就可以解决该问题的方法呢?答案是有的,利用的是 单调栈 这一数据结构。具体的解法思路是这样的:
- 建立一个栈中元素为
height索引的单调栈stk,每个索引对应的高度从栈底到栈顶严格单调递减。- 例:
stk = [0, 1, 2, 5],这意味着height[0] > height[1] > height[2] > height[5]。
- 例:
- 从左侧开始遍历
height,获取当前索引i和当前高度cur_h。针对以下两种情况:stk为空,将i入栈,继续遍历。stk不为空,进入第三步。
- 比较当前高度
cur_h和栈顶索引所对应的高度height[stk[-1]]的大小:cur_h < height[stk[-1]],将i入栈,继续遍历。cur_h >= height[stk[-1]],进入第四步。
- 按以下步骤循环,直至
stk为空或者栈顶索引对应的高度大于等于当前高度:- 将栈顶元素弹出,它在
height中所对应的是目前所在的局部区间内的最小高度,记为lowest = height[stk.pop()]。此时:- 若
stk为空,退出循环,将i入栈。 - 若
stk不为空,此时栈顶元素对应的高度是一个局部”凹”字形结构的左边界,那么这个结构内可以积的水可以按照如下方式计算:- 左右边界的距离
d = i - stk[-1] - 1 - 积水高度
h = min(height[stk[-1]], cur_h) - lowest - 则积水量为上述两个数相乘,将计算出来的积水量加到最终的结果
ans中。
- 左右边界的距离
- 若
- 将栈顶元素弹出,它在
上述流程比较复杂,不如来看一个实际的例子,相信对于这个解法的理解会更有帮助。
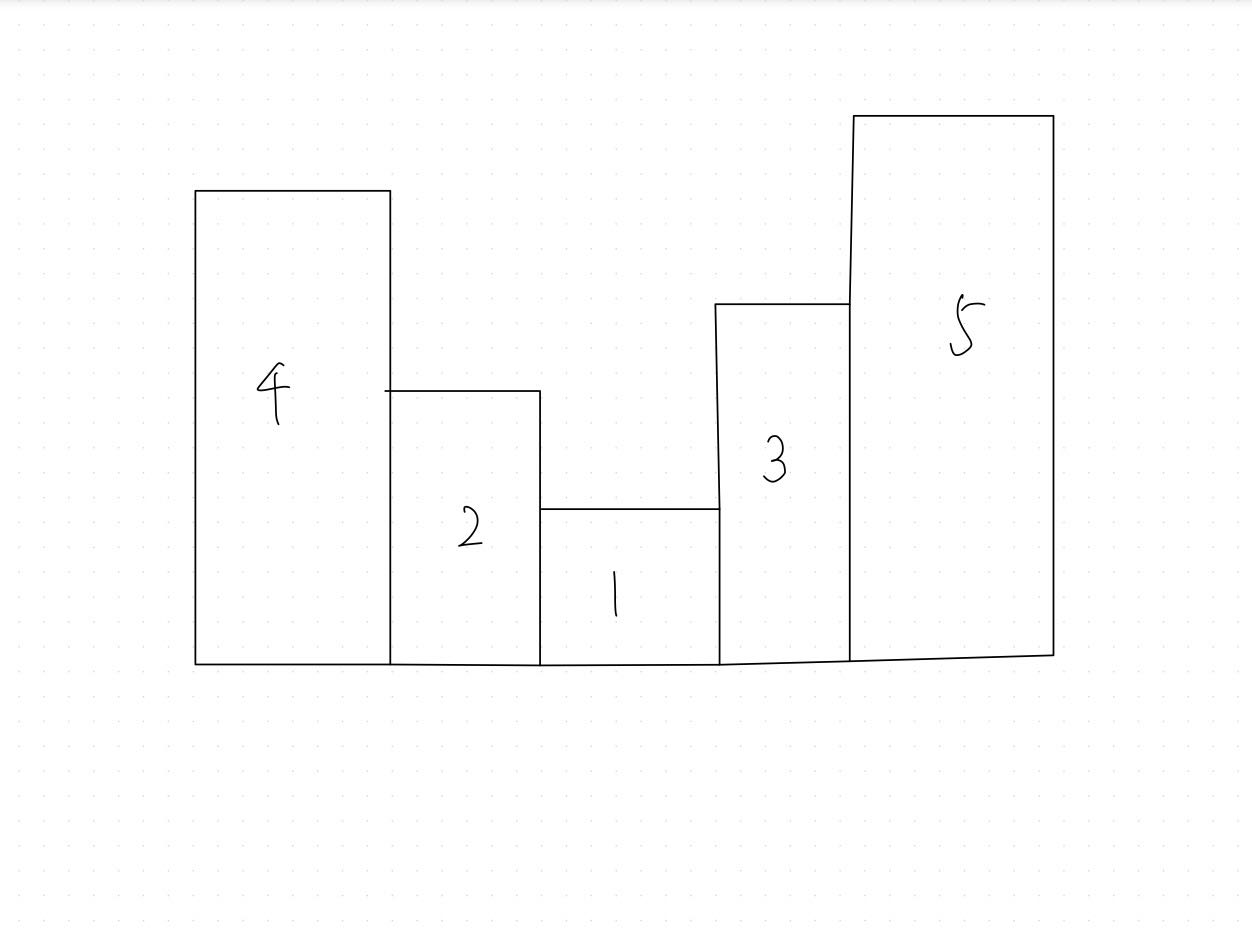
现在假设: height = [4, 2, 1, 3, 5],此时建立一个单调栈stk = []。接下来对height中的索引和高度进行遍历:
- 遍历至: $4$ ,索引为: $0$
stk = []- 操作:将索引
0入栈,继续遍历
- 遍历至: $2$ ,索引为: $1$
stk = [0],栈顶索引对应的高度为 $4$- 当前高度: $2$ ,小于栈顶索引对应的高度
- 操作:将索引
1入栈,继续遍历
- 遍历至: $1$ ,索引为: $2$
stk = [0, 1],栈顶索引对应的高度为 $2$- 当前高度: $1$ ,小于栈顶索引对应的高度
- 操作:将索引
2入栈,继续遍历
- 遍历至: $3$ ,索引为: $3$
stk = [0, 1, 2],栈顶索引对应的高度为 $1$- 当前高度: $3$ ,大于栈顶索引对应的高度,进入出栈循环
出栈循环开始
- 将栈顶索引弹出,得到最低积水水位: $1$
stk = [0, 1],栈顶元素对应的高度为 $2$- 当前高度: $3$ ,大于栈顶索引对应的高度
- 计算当前可积水量:
- 左右边界距离
d = i - stk[-1] - 1 = 3 - 1 - 1 = 1 - 积水高度
h = min(height[stk[-1]], cur_h) - lowest = min(2, 3) - 1 = 2 - 1 = 1 - 积水量
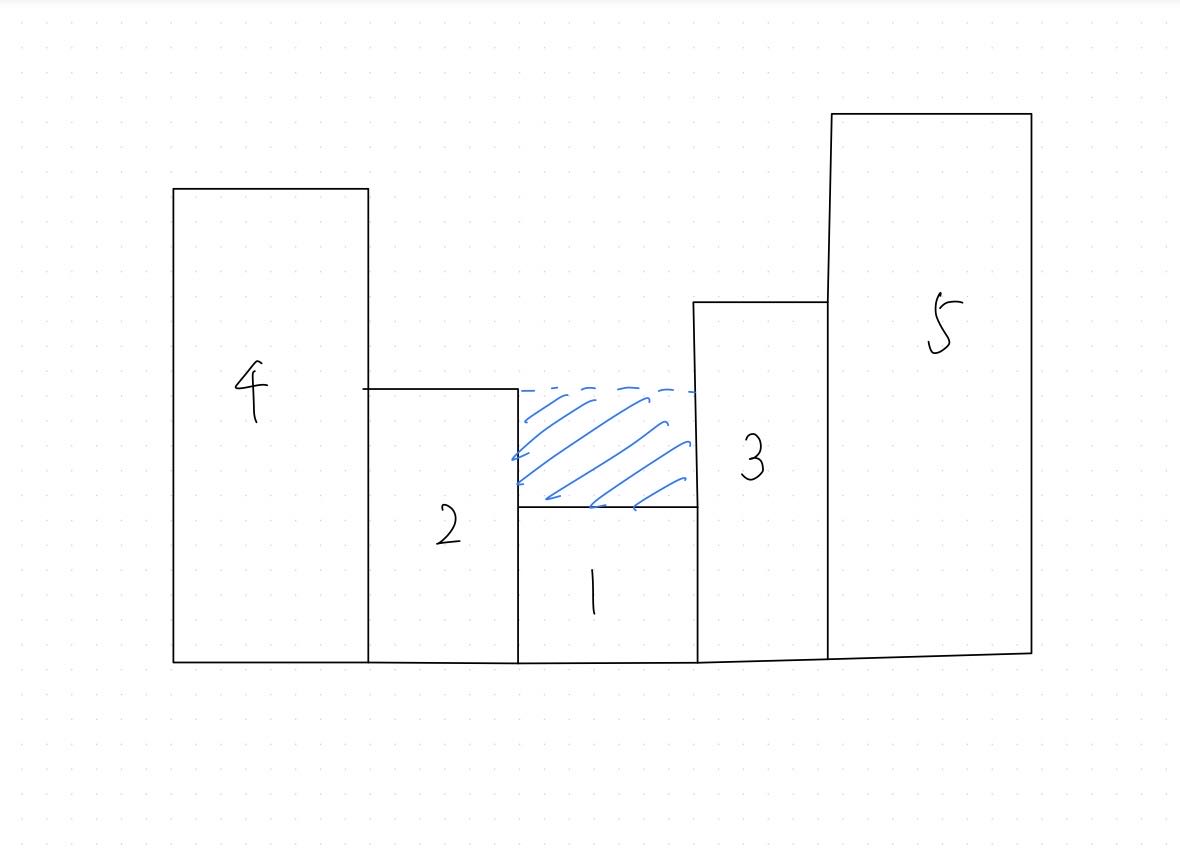
d * h = 1 * 1 = 1,加入到最终答案ans中 - 此时计算的积水部分为蓝色区域:
- 左右边界距离
- 将栈顶索引弹出,得到最低积水水位: $2$
stk = [0],栈顶元素对应的高度为 $4$- 当前高度: $3$ ,小于栈顶索引对应的高度,完成下述计算后退出出栈循环
- 计算当前可积水量:
- 左右边界距离
d = i - stk[-1] - 1 = 3 - 0 - 1 = 2 - 积水高度
h = min(height[stk[-1]], cur_h) - lowest = min(4, 3) - 2 = 3 - 2 = 1 - 积水量
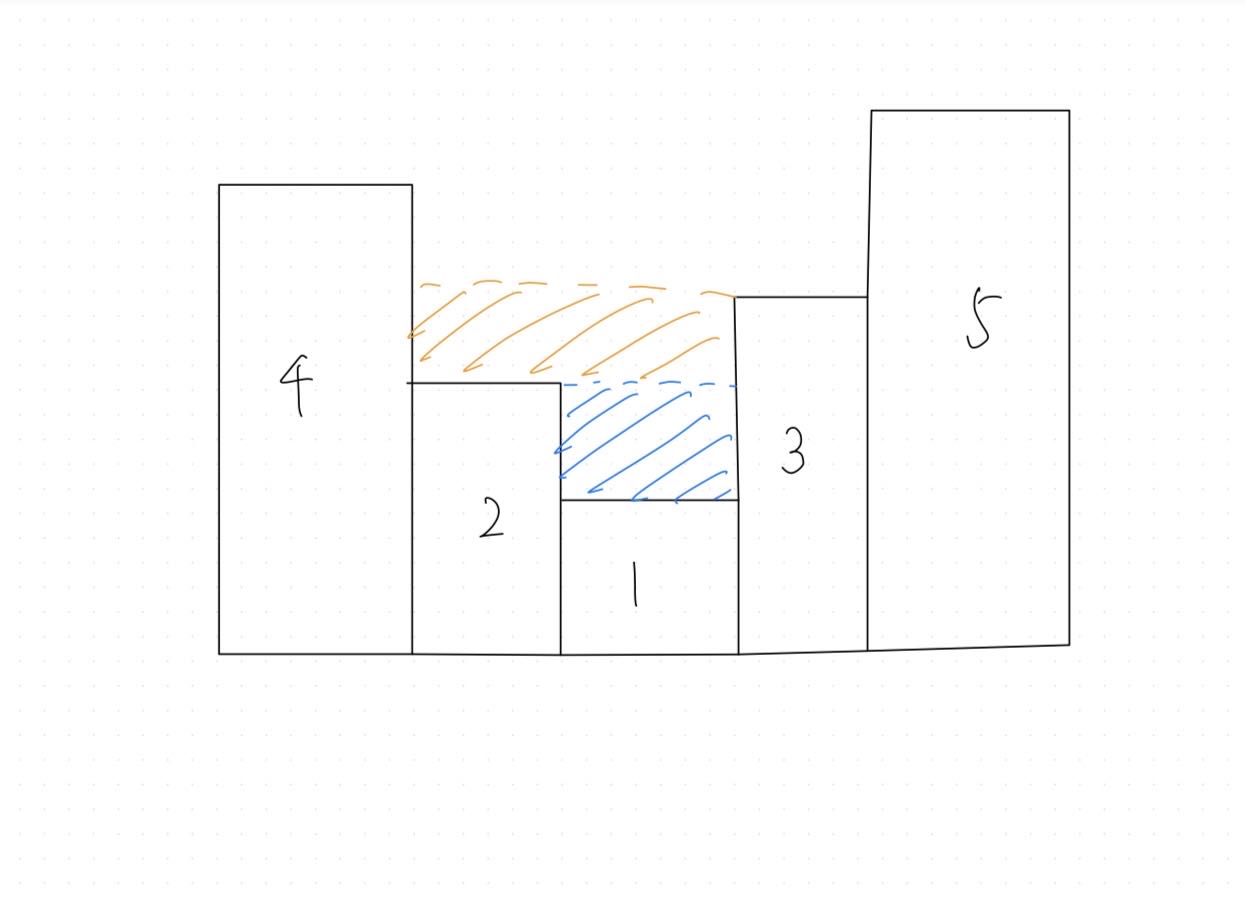
d * h = 2 * 1 = 2,加入到最终答案ans中 - 此时计算的积水部分为橙色区域:
- 左右边界距离
出栈循环结束
将当前索引入栈:
stk = [0, 3]遍历至: $5$ ,索引为: $4$
stk = [0, 3],栈顶索引对应的高度为 $3$- 当前高度: $5$ ,大于栈顶索引对应的高度,进入出栈循环
出栈循环开始
- 将栈顶索引弹出,得到最低积水水位: $3$
stk = [0],栈顶元素对应的高度为 $4$- 当前高度: $5$ ,大于栈顶索引对应的高度
- 计算当前可积水量:
- 左右边界距离
d = i - stk[-1] - 1 = 4 - 0 - 1 = 3 - 积水高度
h = min(height[stk[-1]], cur_h) - lowest = min(4, 5) - 3 = 4 - 3 = 1 - 积水量
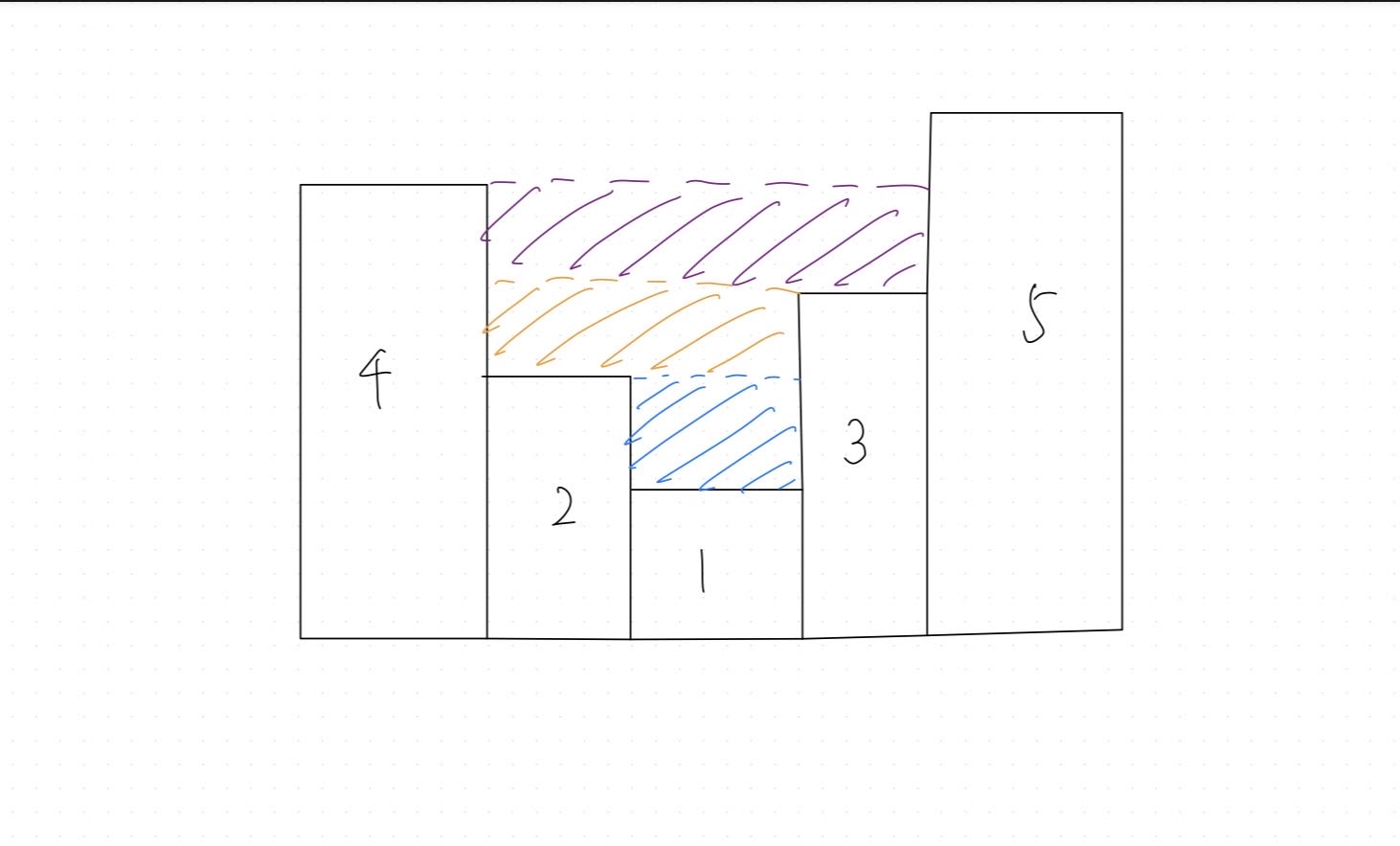
d * h = 3 * 1 = 2,加入到最终答案ans中 - 此时计算的积水部分为紫色区域:
- 左右边界距离
- 将栈顶索引弹出,得到最低积水水位: $4$
stk = [],栈为空,break
出栈循环结束
- 将当前索引入栈:
stk = [5] - 遍历结束,返回结果
如此,整个算法流程结束。通过流程中的图片我们可以发现这个解法计算积水量的方式与前两者不同,它并不是针对每一个点位计算其可能积水的量,而是先确认可以积水的范围,再通过层层叠加的方式计算积水量。
该解法的代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
def trap(self, height: List[int]) -> int:
stk = []
ans = 0
for i, cur_h in enumerate(height):
while stk and cur_h > height[stk[-1]]:
lowest = height[stk.pop()]
if not stk:
break
d = i - stk[-1] - 1
ans += (min(height[stk[-1]], cur_h) - lowest) * d
stk.append(i)
return ans
结果顺利通过。
Time complexity: $O(n)$
Space complexity: $O(n)$
解法四:双指针
解法二 中用两个数组分别存储了对应点位两侧的最高高度,事实上这一步还可以进一步优化。我们可以在记录两侧最高高度的同时,直接完成对每个点位积水量的计算。要做到这一点,需要同时从height两侧进行遍历,那么双指针的使用便成为一个必然的选择。指针在移动时需要遵循以下两点:
- 每个指针记录下遍历过程中迄今为止遇到的最高高度
- 当前所处高度更低的指针优先行进
下面针对以上两个原则进行解说。第一个原则是为了实现解法二中对于积水区域两侧边界高度的记录。第二个原则是依据木桶原理,也即一个点位的积水高度永远取决于两侧边界中高度更低的那一个,优先移动更低侧的指针可以确保计算积水高度时该侧指针记录过的最高高度为木桶的“短板”。我们来看一下具体的代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
# 左右两侧指针各自需要记录的已访问的点位中的最高高度
left_max, right_max = 0, 0
# 左右指针
l, r = 0, n - 1
ans = 0
while l < r:
# 遵循低位指针优先移动的原则,此时左指针高度更低,优先移动
if height[l] <= height[r]:
# 更新已访问点位中的最高高度
left_max = max(left_max, height[l])
# 雨水高度取决于低侧的已访问最高高度
ans += left_max - height[l]
l += 1
# 遵循低位指针优先移动的原则,此时右指针高度更低,优先移动
else:
right_max = max(right_max, height[r])
ans += right_max - height[r]
r -= 1
return ans
如此,我们便可以在一次遍历中直接完成积水量的计算,并且只需用到常数量级的空间。
结果顺利通过。
Time complexity: $O(n)$
Space complexity: $O(1)$
总结
经典的面试高频题,问题的核心在于积水高度始终遵循木桶原理,以及如何在实际计算过程中获取“短板”的高度。题解依次按照暴力解法、动态规划、单调栈、双指针的思路逐步完成优化,非常值得反复品味。