题目概述
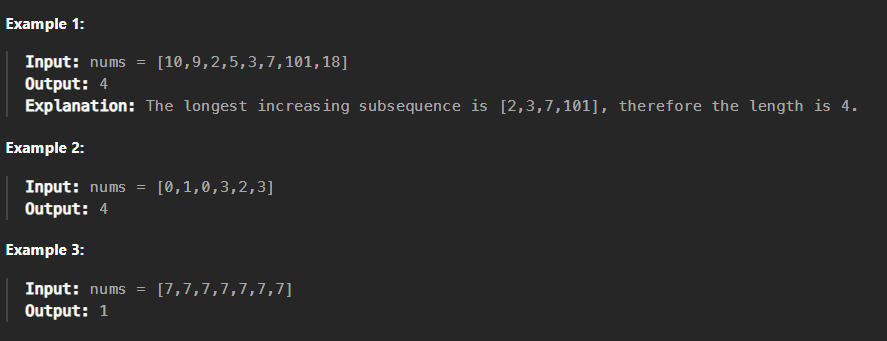
Given an integer array nums, return the length of the longest strictly increasing subsequence.
A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
Constraints:
1 <= nums.length <= 2500-10 ^ 4 <= nums[i] <= 10 ^ 4
思路 & 代码实现
这里明确一下 subsequence(子序列) 和 subarray(子数组) 的区别。两者均是原数组中元素的一个子集(前提是数组中元素相对位置保持不变)。区别在于,子序列不要求元素在原数组中是连续的,而子数组则必须是原数组中一个连续的子集。
解法一:动态规划
对于这道题来说,使用动态规划是一个经典的做法。我们可以维护一个一维的 dp 数组,其中 dp[i] 定义的状态为:结尾为 nums[i] 的最长递增子序列的长度。 对于所有的状态来说,这个结果的最小值均为1,因为最差的情况下(从原数组第一个元素到 nums[i] 的整个切片范围内的元素单调递减),这个最长递增子序列只包含 nums[i] 本身,长度为1。如果用代码对这一部分进行初始化的话,结果如下所示:
1
2
n = len(nums)
dp = [1] * n
接下来思考状态转移方程。如果我们想要求解 dp[i] ,我们可以 遍历小于 i 的索引 j ,并获取原数组中对应位置的元素的值 nums[j] ,以及结尾为 nums[j] 的最长递增子序列长度 dp[j] 。 随后进行如下操作:
- 如果
nums[i]的值大于nums[j],那么说明nums[i]可以添加到nums[j]后,并与其构成一个严格单调递增的子序列。 - 此时,这个子序列的长度是结尾为
nums[j]的最长递增子序列的长度dp[j]再加上1 - 在遍历的过程中 获取所有满足条件的子序列的长度 ,其中 最长 的那一个便是
dp[i]的值
转换为数学语言:
\[\text{dp}[i] = max(\text{dp}[j] + 1) \qquad \text{if} \; \text{nums}[i] > \; \text{nums}[j], \quad j \in [0, i)\]至此,单个状态的转移已经定义完毕。那么此题最终的答案应该是什么呢?我们可以发现,依照这个状态定义的话,最长递增子序列并不一定要以原数组中最后一个元素结尾,事实上它可以是以其中任意一个元素结尾的。因此,想要求出最终的答案,我们需要求出 dp 数组中的最大值。
接下来看一下代码实现:
1
2
3
4
5
6
7
8
9
10
11
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
dp = [1] * n
for i in range(1, n):
for j in range(i):
if nums[j] < nums[i]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
结果顺利通过。
Time complexity: $O(n^2)$
Space complexity: $O(n)$
解法二:贪心
除了使用动态规划,我们还可以模拟一下构建最长递增子序列的过程。在模拟的过程中我们需要维护一个数组,用于存储一个递增子序列 sequence 。过程可以总结如下:
- 遍历原数组
nums, - 若
sequence为空或其末尾元素小于当前遍历到的元素nums[i],则将nums[i]添加至其末尾 - 若
sequence末尾元素大于等于当前遍历到的元素nums[i],则在其中进行线性搜索,将第一个搜索到的大于nums[i]的元素替换为nums[i]。
这里解释一下第三步操作。首先我们需要明确一点:sequence 中存储的并不是作为答案的那一个最长递增子序列。 但是其长度与最长递增子序列是相同的,由于题目让我们求的正是这个长度,所以该方案是可行的。至于为什么它的长度与最长递增子序列相同,我会在之后说明。
现在让我们着眼于构造递增子序列这一过程本身。可以观察到,只有在原数组遍历到的元素大于 sequence 的末尾元素时,sequence 的长度才会增加。那么为了最大化 sequence 这个数组的长度,我们需要让数值较小的元素尽可能地排入,这样可以 增加后续较大元素进入序列时直接被添加至末尾的可能性 ,以实现增长序列的目的。
我们不妨用一个具体的例子来演示一下整个构建过程。假设原数组 nums 中的元素如下所示:
现在开始遍历这个数组:
蓝色表示 sequence 中需要被替换的元素,橙色表示 sequence 中替换后的元素,绿色表示 sequence 中新添加的元素。
- 遍历至: $10$
sequence:空- 操作:添加至末尾
- 结果:$\textcolor{green}{10}$
- 遍历至: $9$
sequence:$\textcolor{royalblue}{10}$- 操作:替换 $10$
- 结果:$\textcolor{orange}{9}$
- 遍历至: $2$
sequence:$\textcolor{royalblue}{9}$- 操作:替换 $9$
- 结果:$\textcolor{orange}{2}$
- 遍历至: $5$
sequence:$2$- 操作:添加至末尾
- 结果:$2 \quad \textcolor{green}{5}$
- 遍历至: $3$
sequence:$2 \quad \textcolor{royalblue}{5}$- 操作:替换 $5$
- 结果:$2 \quad \textcolor{orange}{3}$
- 遍历至: $7$
sequence:$2 \quad 3$- 操作:添加至末尾
- 结果:$2 \quad 3 \quad \textcolor{green}{7}$
- 遍历至: $101$
sequence:$2 \quad 3 \quad 7$- 操作:添加至末尾
- 结果:$2 \quad 3 \quad 7 \quad \textcolor{green}{101}$
- 遍历至: $4$
sequence:$2 \quad 3 \quad \textcolor{royalblue}{7} \quad 101$- 操作:替换 $7$
- 结果:$2 \quad 3 \quad \textcolor{orange}{4} \quad 101$
- 遍历至: $6$
sequence:$2 \quad 3 \quad 4 \quad \textcolor{royalblue}{101}$- 操作:替换 $101$
- 结果:$2 \quad 3 \quad 4 \quad \textcolor{orange}{6}$
- 遍历至: $18$
sequence:$2 \quad 3 \quad 4 \quad 6$- 操作:添加至末尾
- 结果:$2 \quad 3 \quad 4 \quad 6 \quad \textcolor{green}{18}$
- 遍历至: $1$
sequence:$\textcolor{royalblue}{2} \quad 3 \quad 4 \quad 6 \quad 18$- 操作:替换 $2$
- 结果:$\textcolor{orange}{1} \quad 3 \quad 4 \quad 6 \quad 18$
按照这个流程我们可以得到 sequence 最终的长度为5。
再看一下其中的元素构成,是
\[1 \quad 3 \quad 4 \quad 6 \quad 18\]但事实上真正的最长递增子序列是
\[2 \quad 3 \quad 4 \quad 6 \quad 18\]从这里可以看出 sequence 中保存的并不是正确的那一个最长递增自序列。但是我之前提到其长度是正确的,这是因为这个序列的长度只有在后续元素大于其末尾元素时才会增加,而在逻辑层面上,末尾元素此时已经位于序列中,这说明它在原数组中出现的时机必然早于当前遍历到的尚未被加入序列中的元素。
本质上,我们对于这个序列只存在两种操作:替换元素 和 添加元素,替换元素这个操作会打乱序列中元素在原数组中对应的顺序,而添加元素则不会。因为替换元素这个操作存在,所以我们最后得到的序列并不是真正的最长递增子序列,但是由于 替换元素并不会改变序列长度 ,以及 添加元素不会打乱序列中元素在原数组中对应的顺序 ,所以该序列在长度上的正确性得到了保证。这便是该方法得以成立的原因。
最后我们看一下代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
sequence = []
for num in nums:
if not sequence or sequence[-1] < num:
sequence.append(num)
else:
for i, pre_num in enumerate(sequence):
if pre_num >= num:
sequence[i] = num
return len(sequence)
结果顺利通过。
Time complexity: $O(n^2)$
Space complexity: $O(n)$
解法二优化:贪心 + 二分查找
解法二在 sequence 中寻找待替换元素时使用的是线性搜索,时间复杂度为 $O(n)$ ,但事实上整个 sequence 是有序的,它保持了单调递增。因此,在查找特定元素时可以使用 二分查找 进一步优化。以下为代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
sequence = []
for num in nums:
if not sequence or sequence[-1] < num:
sequence.append(num)
else:
l, r = 0, len(sequence) - 1
while l <= r:
mid = l + (r - l) // 2
if sequence[mid] < num:
l = mid + 1
else:
r = mid - 1
sequence[l] = num
return len(sequence)
或使用python的 bisect 库中的 bisect_left 函数替换手动实现部分:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from bisect import bisect_left
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
sequence = []
for num in nums:
if not sequence or sequence[-1] < num:
sequence.append(num)
else:
update_id = bisect_left(sequence, num)
sequence[update_id] = num
return len(sequence)
结果顺利通过。
Time complexity: $O(nlog(n))$
Space complexity: $O(n)$