Leetcode 1926 距离迷宫入口最近的出口

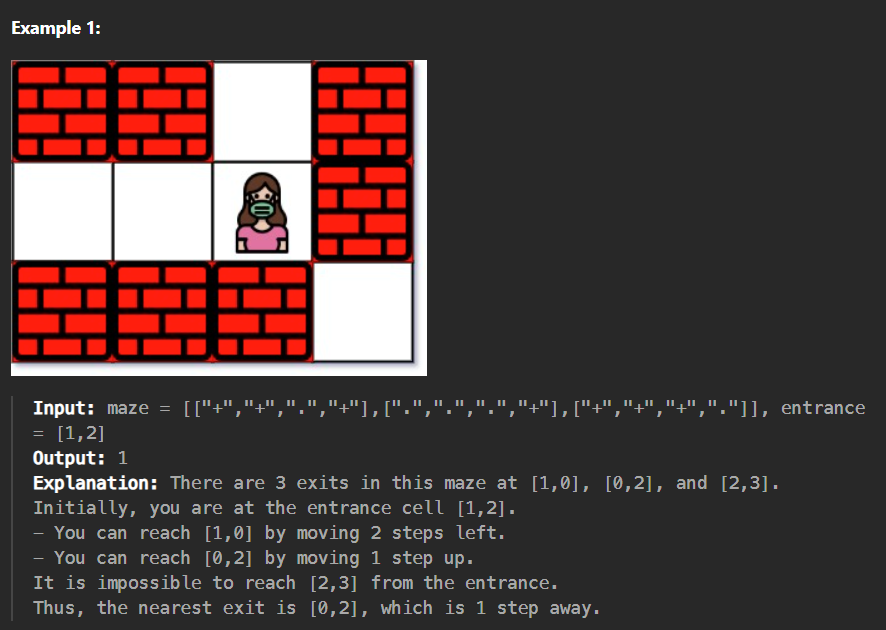
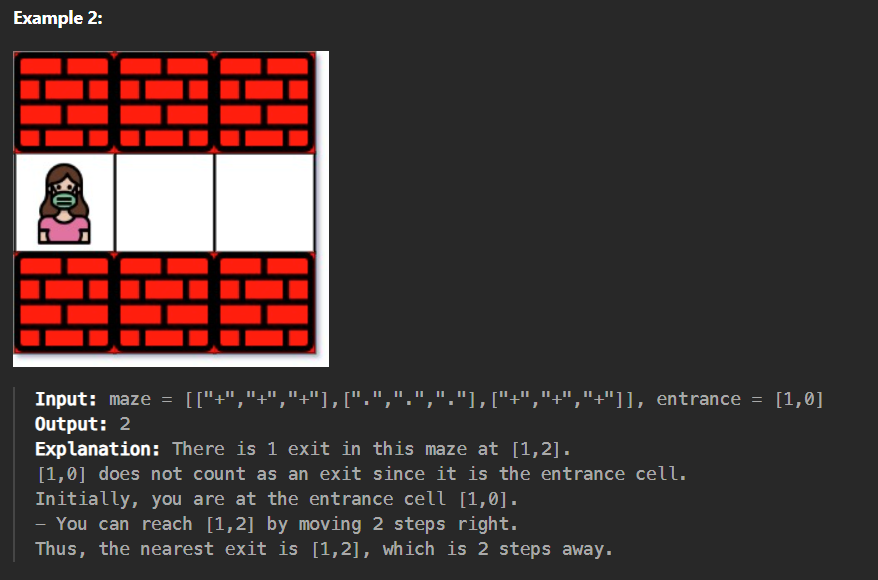
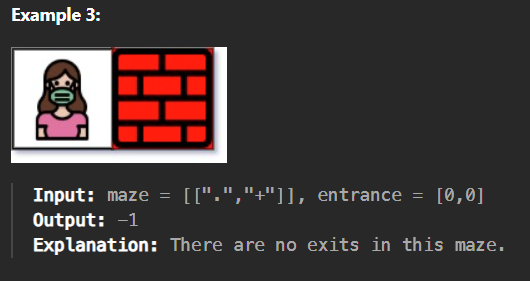
题目概述

Leetcode 1926

You are given an m x n matrix maze (0-indexed) with empty cells (represented as '.') and walls (represented as '+'). You are also given the entrance of the maze, where entrance = [entrance_row, entrance_col] denotes the row and column of the cell you are initially standing at.

In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.

Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.

Constraints:

• maze.length == m
• maze[i].length == n
• 1 <= m, n <= 100
• maze[i][j] is either '.' or '+'.
• entrance.length == 2
• 0 <= entrance_row < m
• 0 <= entrance_col < n
• entrance will always be an empty cell.

思路

这道题的思路很明确，就是使用BFS进行寻路，一旦找到符合要求的出口就结束探索，并返回入口与出口的距离。具体的探索过程使用队列 + 迭代。此外还需要一个visited数组记录已访问的迷宫节点，避免重复搜索进入死循环。这里先写出进入探索过程前的代码，主要内容是各种变量的初始化。

# get the size of the maze      
m, n = len(maze), len(maze[0])  

# initialize the visited array  
visited = [[False] * n for _ in range(m)]
        
# right, down, left, up 
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]

# initialize the queue for BFS, 0 is used for memorizing distance
queue = [[entrance, 0]]

接下来就是进入探索过程的部分了。这里的思路是：当队列不为空时，说明探索尚未结束，此时将队列首个元素弹出作为此次探索的目的地，并在visited数组中记录此次探索的位置。若此次探索的位置正好是出口，则直接返回对应的距离；若不是则继续遍历四个方向，将其中所有符合要求的节点都添加至队列中（注意更新距离）以进行后续的探索。当探索结束时若仍未返回任何距离值，则说明从题目给定的入口出发无法抵达迷宫的任意一个出口，此时按照题目要求返回-1。整个过程的代码如下:

while queue:
	(i, j), dis = queue.pop(0)

	# exit has been found
	if (i == 0 or j == 0 or i == m-1 or j == n-1) and [i, j] != entrance:
		return dis

	# memorize the position that has been visited
	visited[i][j] = True

	# search next available steps
	for di, dj in directions:
		ii, jj = i + di, j + dj
		if 0 <= ii < m and 0 <= jj < n and maze[ii][jj] != "+" and not visited[ii][jj]:
			queue.append([[ii, jj], dis+1])

# exit can not be reached from the given entrance, so return -1
return -1

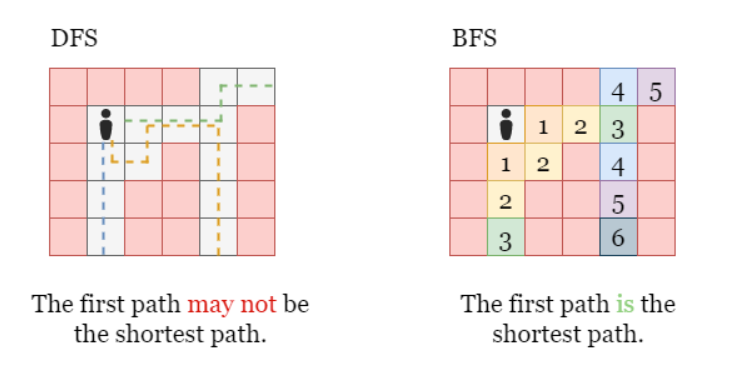
至于为什么在发现第一个出口时就直接返回距离，而不是将其与剩余可能存在的出口的距离进行比较，是因为根据BFS的特性，搜索范围是以起点为中心均匀向四周发散的，搜索的范围随着时间的增加而增加，这也就意味着第一个（所花时间最少）被搜索到的结果必定是距离起点最近的。也就是说BFS天然适合这类寻找最短路径的问题。下图说明了对于这类问题使用DFS和BFS的区别。

将上文中两部分代码整合到一起便是最终的答案了。提交结果：Time Limit Exceeded!

错误原因分析

结果和预想的不一样。这道题并没有说迷宫具有什么特殊性，所以初步推断BFS这个思路本身应该是没有问题的。那么问题到底出在哪里了呢？由于思考了一段时间并没有什么结果，所以我去看了一眼discussion里有没有人给出一些提示。没想到果然有，给出的提示是改变将访问的节点记录至visited数组的时机。

不得不说，这还真是一个以前没怎么仔细考虑过的点。考虑修改visited数组的时机的话，有以下两种方式：

• 元素出队列时修改
• 元素入队列时修改

不妨比较一下两者有什么区别，这里就假设探索起点位于(0, 0)，且整个探索范围无墙壁等阻碍。那么对于第一种方式，记录每个位置入队列的次数，有：

\[\begin{aligned} \begin{matrix} \color{lime}{1} & \rightarrow & \color{yellow}{1} & \rightarrow & \color{orange}{1} & \rightarrow & \color{red}{1} & \rightarrow & \color{purple}{1} & \rightarrow & \cdots \\ \downarrow & & \downarrow & & \downarrow & & \downarrow & & \downarrow \\[1mm] \color{yellow}{1} & \rightarrow & \color{orange}{2} & \rightarrow & \color{red}{3} & \rightarrow & \color{purple}{4} & \rightarrow & \cdots \\ \downarrow & & \downarrow & & \downarrow & & \downarrow \\[1mm] \color{orange}{1} & \rightarrow & \color{red}{3} & \rightarrow & \color{purple}{6} & \rightarrow & \cdots \\ \downarrow & & \downarrow & & \downarrow \\[1mm] \color{red}{1} & \rightarrow & \color{purple}{4} & \rightarrow & \cdots \\ \downarrow & & \downarrow \\[1mm] \color{purple}{1} & \rightarrow & \cdots \\ \downarrow \\[1mm] \cdots \end{matrix} \end{aligned}\]

显然，随着搜索范围不断扩大，新元素入队列的次数按照二次函数形式增长。这里就发现先前解法不够完善的地方了：对于元素的入队列次数并没有进行限制，导致大量无效操作。那么如果采用第二种方式的话结果又如何呢？

\[\begin{aligned} \begin{matrix} \color{orange}{1} & \rightarrow & \color{orange}{1} & \rightarrow & \color{orange}{1} & \rightarrow & \color{orange}{1} & \rightarrow & \color{orange}{1} & \rightarrow & \cdots \\ \downarrow & & \downarrow & & \downarrow & & \downarrow & & \downarrow \\[1mm] \color{orange}{1} & \xcancel{\rightarrow} & \color{orange}{1} & \xcancel{\rightarrow} & \color{orange}{1} & \xcancel{\rightarrow} & \color{orange}{1} & \rightarrow & \cdots \\ \downarrow & & \downarrow & & \downarrow & & \downarrow \\[1mm] \color{orange}{1} & \xcancel{\rightarrow} & \color{orange}{1} & \xcancel{\rightarrow} & \color{orange}{1} & \xcancel{\rightarrow} & \cdots \\ \downarrow & & \downarrow & & \downarrow \\[1mm] \color{orange}{1} & \xcancel{\rightarrow} & \color{orange}{1} & \xcancel{\rightarrow} & \cdots \\ \downarrow & & \downarrow \\[1mm] \color{orange}{1} & \xcancel{\rightarrow} & \cdots \\ \downarrow \\[1mm] \cdots \end{matrix} \end{aligned}\]

可以看到，按照第二种方式的话，下一步可探索的位置在被加入队列后随即就被标记为visited，这样后续的点探索时就不会重复地将大量无效的元素加入队列了。

代码实现

那么按照上文中第二种方式探索的话，代码就应修改成:

Time complexity: O(mn)

Space complexity: O(mn)

m, n = len(maze), len(maze[0])
visited = [[False] * n for _ in range(m)]
visited[entrance[0]][entrance[1]] = True
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
queue = [[entrance, 0]]

while queue:
	(i, j), dis = queue.pop(0)
	if (i == 0 or j == 0 or i == m-1 or j == n-1) and [i, j] != entrance:
		return dis
	for di, dj in directions:
		ii, jj = i + di, j + dj
		if 0 <= ii < m and 0 <= jj < n and maze[ii][jj] != "+" and not visited[ii][jj]:
			queue.append([[ii, jj], dis+1])
			visited[ii][jj] = True

return -1        

顺利通过。

事实上，visited数组在这道题完全可以被摒弃。还有另一种方式既能节省空间，又能使代码更加简洁，那就是：待探索位置入队列时，直接将迷宫里对应该位置的标记修改为"+"，也就是视作一堵墙。这样起到的作用与利用visited数组是等效的，都是为了避免探索回头路。代码如下：

Time complexity: O(mn)

Space complexity: O(max(m, n))

class Solution:
    def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:
        m, n = len(maze), len(maze[0])
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        queue = [[entrance, 0]]

        while queue:
            (i, j), dis = queue.pop(0)
            if (i == 0 or j == 0 or i == m-1 or j == n-1) and [i, j] != entrance:
                return dis
            for di, dj in directions:
                ii, jj = i + di, j + dj
                if 0 <= ii < m and 0 <= jj < n and maze[ii][jj] != "+":
                    queue.append([[ii, jj], dis+1])
                    maze[ii][jj] = "+"

        return -1