题目概述
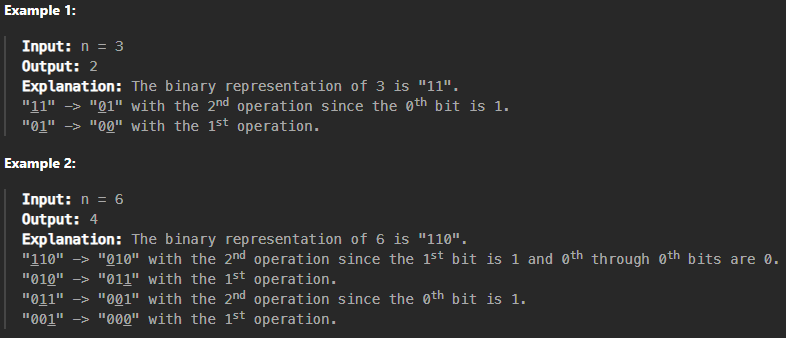
Given an integer n, you must transform it into 0 using the following operations any number of times:
- Change the rightmost (
0th) bit in the binary representation ofn. - Change the
ithbit in the binary representation ofnif the(i-1)thbit is set to1and the(i-2)ththrough0thbits are set to0.
Return the minimum number of operations to transform n into 0.
Constraints:
0 <= n <= 10^9
思路 & 代码实现
BFS
首先,根据题意得知对于一个二进制整数我们可以进行两种操作。题目中对于操作的叙述有些晦涩,所以让我们换一种简单易懂的说法:
- 操作1:修改该二进制整数最右位的数字,也就是将1替换成0,或者将0替换成1
操作2: 找到该二进制整数所有位中位于最右侧的1,然后修改与其相邻并位于其左侧的那一位数字,例如:
\[\begin{aligned} 10110100 & \rightarrow 1011{\color{red}{1}}100 \\ 0001 & \rightarrow 00{\color{red}{1}}1 \end{aligned}\]
现在的目标是利用这两种操作将给定的整数变换成0,并且希望操作数尽可能地少。此时脑海中浮现出的是一个非常朴素的做法:将两种操作函数化,随后对给定的整数进行操作流程上的BFS探索,直至操作结果为0时结束探索并输出答案。 为了实现这个想法,首先需要做的是如何将上述两种操作分别表现为函数的形式。
对于第一种操作,我们可以观察得到其实就是将给定整数与1进行异或运算,故有:
1
2
def op1(x):
return x ^ 1
对于第二种操作则复杂一些,首先需要找到给定整数的最右位的1在何处,此时我又想到之前在做统计一个二进制整数中1的个数这个问题时用到的一个技巧:
1
x &= x - 1
举一个例子:
\[\begin{array}{c} & 11000100100 \\ \& & 11000100011 \\ \hline & 11000100{\color{red}{000}} \end{array}\]可以看出这个技巧的作用是对于给定整数,将其最右侧的1移除。那么如果将原本给定的整数与这个结果做差,不就可以得到被删除的那一位,也就是我们想要的最右位的1了吗!在此基础上需要将这个最右位的1的左侧相邻位进行修改,也就是将这个最右位的1左移一位,并与原本给定的整数进行异或运算,总结成代码如下:
1
2
3
def op2(x):
rightmost_one = x - (x & (x - 1))
return x ^ (rightmost << 1)
接下来就是探索的部分,采用BFS的原因是可以保证在第一次变换操作得到0时就能输出正确的结果,也就是最少的操作数。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
def minimumOneBitOperations(self, n: int) -> int:
def op1(x):
return x ^ 1
def op2(x):
rightmost_one = x - (x & (x - 1))
return x ^ (rightmost_one << 1)
ans = 0
q = deque([n])
visited = set([n])
# BFS
while q:
for _ in range(len(q)):
num = q.popleft()
if not num:
return ans
num_op1, num_op2 = op1(num), op2(num)
if num_op1 not in visited:
visited.add(num_op1)
q.append(num_op1)
if num_op2 not in visited:
visited.add(num_op2)
q.append(num_op2)
ans += 1
但是这种比较暴力的做法很显然效率不高,并且会MLE (Memory Limit Exceed)。
DFS
随后我想是否能将其转化成DFS的形式,并最终简化成动态规划。转换成DFS的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
def minimumOneBitOperations(self, n: int) -> int:
def op1(x):
return x ^ 1
def op2(x):
rightmost_one = x - (x & (x - 1))
return x ^ (rightmost_one << 1)
self.start = n
visited = set()
# DFS
def dp(n):
if n == 0:
return 0
if n >= (self.start << 1):
return inf
if n in visited:
return inf
visited.add(n)
num_op1, num_op2 = op1(n), op2(n)
return min(dp(num_op1), dp(num_op2)) + 1
return dp(n)
这里细节比较多,所以一处一处说:
self.start在这里的作用是记录最开始的给定整数,而我们可以看到在dp函数中有这样一段代码:1 2
if n >= self.start * 2: return inf
这是为了防止操作2将原本的数无意义地增大,看一下例子:
\[\begin{aligned} & 0100 \\ & {\color{red}{1}}100 \end{aligned}\]这里使用操作2的话不仅没有消去最左边一位的1,还在其左侧又添加了一个1,属于对于解题无意义的操作,因此需要设法规避,否则需要的操作的数会在探索的过程中越变越大,导致探索无法终结。规避的条件就是判断操作后的结果是否不小于直接左移一位的结果。
visited这个集合在BFS的代码中也出现了,它是为了记录已经探索过的数,避免走回头路。最后返回的结果是
min(dp(num_op1), dp(num_op2)) + 1,为了理解这一步,我们首先需要思考一下dp这个函数本身的含义。dp(n)表示的是对于n这个数,将其变换为0所需的最少操作数。num_op1和num_op2分别表示的是对n进行操作1和操作2之后得到的结果。所以dp(num_op1)和dp(num_op2)表示的就分别是:dp(num_op1),对n进行操作1之后,后续所需的最少操作数dp(num_op2),对n进行操作2之后,后续所需的最少操作数
很显然,
dp(n)的结果对应的就是上述两种后续最少操作数中更小的那一个,加上进行操作1或者操作2的这一步操作。
光是完成了DFS还是不够的,效率本质上并没有提升。接下来让我思考很久的就是如何将DFS转换成动态规划的形式。一般来说当这个DFS函数拥有返回值时可以根据输入和输出值的形式得出状态转移方程,类似的内容可以参照这篇文章。对于这一题,我们可以得出状态转移方程应该是dp(n) = min(dp(op1(n)), dp(op2(n))) + 1。但是可以观察到这个变换并不一直沿着同一个方向,这里的方向指的就是变换前后数的大小指向关系,也就是说,操作后的数有可能变大也可能变小,因而无法通过简单的迭代去实现动态规划。
题解
到这一步为止,由于本人能力有限,已经无法更进一步地思考或者寻找到别的思路,遂看了此题的第一个提示:
- The fastest way to convert n to zero is to remove all set bits starting from the leftmost one. Try some simple examples to learn the rule of how many steps are needed to remove one set bit.
其中的一个关键词是:消去最左侧的1。让我们从找规律开始,重新审视这个问题,从所有位中只有一个1的情况开始,也就是给定整数为2的整数次幂的时候,操作的过程如下所示:
\[\begin{aligned} & \overset{\color{orange}{1}}{\underset{\color{royalblue}{1}}{1}} \rightarrow \overset{\color{orange}{0}}{\underset{\color{royalblue}{0}}{0}} \\ \\ & \overset{\color{orange}{3}}{\underset{\color{royalblue}{2}}{10}} \rightarrow \overset{\color{orange}{2}}{\underset{\color{royalblue}{3}}{11}} \rightarrow \overset{\color{orange}{1}}{\underset{\color{royalblue}{1}}{01}} \rightarrow \overset{\color{orange}{0}}{\underset{\color{royalblue}{0}}{00}} \\ \\ & \overset{\color{orange}{7}}{\underset{\color{royalblue}{4}}{100}} \rightarrow \overset{\color{orange}{6}}{\underset{\color{royalblue}{5}}{101}} \rightarrow \overset{\color{orange}{5}}{\underset{\color{royalblue}{7}}{111}} \rightarrow \overset{\color{orange}{4}}{\underset{\color{royalblue}{6}}{110}} \rightarrow \overset{\color{orange}{3}}{\underset{\color{royalblue}{2}}{010}} \rightarrow \overset{\color{orange}{2}}{\underset{\color{royalblue}{3}}{011}} \rightarrow \overset{\color{orange}{1}}{\underset{\color{royalblue}{1}}{001}} \rightarrow \overset{\color{orange}{0}}{\underset{\color{royalblue}{0}}{000}} \\ \\ & \overset{\color{orange}{15}}{\underset{\color{royalblue}{8}}{1000}} \rightarrow \overset{\color{orange}{14}}{\underset{\color{royalblue}{9}}{1001}} \rightarrow \overset{\color{orange}{13}}{\underset{\color{royalblue}{11}}{1011}} \rightarrow \overset{\color{orange}{12}}{\underset{\color{royalblue}{10}}{1010}} \rightarrow \overset{\color{orange}{11}}{\underset{\color{royalblue}{14}}{1110}} \rightarrow \overset{\color{orange}{10}}{\underset{\color{royalblue}{15}}{1111}} \rightarrow \overset{\color{orange}{9}}{\underset{\color{royalblue}{13}}{1101}} \rightarrow \overset{\color{orange}{8}}{\underset{\color{royalblue}{12}}{1100}} \rightarrow \overset{\color{orange}{7}}{\underset{\color{royalblue}{4}}{0100}} \rightarrow \cdots \end{aligned}\]流程图中二进制整数上方的 橙色 数字表示 将当前数字变为0所需的最少操作数 , 而下方的 蓝色 数字则表示 该二进制整数的十进制表示 。根据这张流程表可以总结出以下规律:
- 对于2的整数次幂 $2^k$ ,其所需的最少操作数为 $2^{k+1} - 1$
- 对于2的整数次幂 $2^k$ ,在对其进行的后续 $2^k - 1$ 次操作内,得到的十进制数会在 $[2^k + 1, 2^{k+1}-1]$ 这个范围内无遗漏且不重复地出现
目前较为直观的规律就是上述的这两条。根据当前已有的信息我们可以计算出:当输入值n为2的整数次幂时所需的最少操作数。那么当输入值不是2的整数次幂时又该如何去计算呢?这时就该对第二条规律进行深挖了。考虑到后续十进制数会在 $[2^k + 1, 2^{k+1}-1]$ 这个范围内无遗漏且不重复出现这个特点,或许其与 $2^k$ 的余数可以拿来做一做文章,因为计算得到的每一个余数也都是独一无二的,或许会存在某种对应关系。我们考察一下 $k = 3, 2^k = 8$ 的情况, 不妨设 $f(n)$ 为将n变为0所需的最少操作数:
后续的第一个数为 $9$ ,有
\[{\color{orange}{9 \; \% \; 8 = 1}}, {\color{royalblue}{f(8) = 15, f(9) = 14}}\]此时看不出什么规律
后续的第二个数为 $11$ ,有
\[{\color{orange}{11 \; \% \; 8 = 3}}, {\color{royalblue}{f(8) = 15, f(11) = 13}}\]可以看出两者的差并不与余数相等,两者差为3,而如果将余数3代入 $f$ 则可以的得到 $\color{orange}{f(3) = 2}$ 。可以发现
\[{\color{royalblue}{f(11) = f(8)}} {\color{orange}{- f(11 \% 8)}}\]后续的第三个数为 $10$ ,有
\[{\color{orange}{10 \; \% \; 8 = 2}}, {\color{royalblue}{f(8) = 15, f(10) = 12}}\]两者差为3,如果将余数2代入 $f$ 则可以的得到 $\color{orange}{f(2) = 3}$ 。可以发现
\[{\color{royalblue}{f(10) = f(8)}} {\color{orange}{- f(10 \% 8)}}\]后续的第四个数为 $14$ , 有
\[\color{royalblue}{14 \; \% \; 8 = 6, f(8) = 15, f(14) = 11}\]两者差为4,如果将余数6代入 $f$ 则可以得到 $\color{orange}{f(6) = 4}$ 。可以发现
\[{\color{royalblue}{f(14) = f(8)}} {\color{orange}{- f(14 \% 8)}}\]…
于是可以得出这个函数最终求值是通过递归的方式,而如果令输入值为 $n$ ,令不超过 $n$ 的最大的2的整数次幂为 $k$ ,则有:
\[\begin{aligned} f(n) &= f(k) - f(n \; \% \; k) \\[3mm] &= 2 ^ {k + 1} - 1 - f(n \; \% \; k) \quad \cdots \quad (n > 0) \end{aligned}\]合理性
未完待续。。。
其代码实现为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
def minimumOneBitOperations(self, n: int) -> int:
def get_largest_power_of_two(x):
x |= (x >> 1)
x |= (x >> 2)
x |= (x >> 4)
x |= (x >> 8)
x |= (x >> 16)
return x ^ (x >> 1)
def f(n):
if n == 0:
return 0
m = get_largest_power_of_two(n)
return (m << 1) - 1 - f(n % m)
return f(n)
其中,
1
2
3
4
5
6
7
def get_largest_power_of_two(x):
x |= (x >> 1)
x |= (x >> 2)
x |= (x >> 4)
x |= (x >> 8)
x |= (x >> 16)
return x ^ (x >> 1)
这一部分为求不超过x的最大2的整数次幂的函数。因为输入的x最大不会超过 $10^9$ ,所以只需要32位的二进制数即可表示出所有符合条件的x。上述函数是先将x所有位中最左侧的1以右的所有位都变换成1,然后将最左侧以右所有的1通过异或操作变换为0,以得到2的整数次幂。这样计算比使用迭代要高效。
结果顺利通过。
附录
此问题其实就是将二进制数转换为 格雷码 (Gray code) 的问题,源于中国的传统智力游戏九连环与其的原理也是一致的,此外格雷码也可以用于解汉诺塔问题。
参考链接: