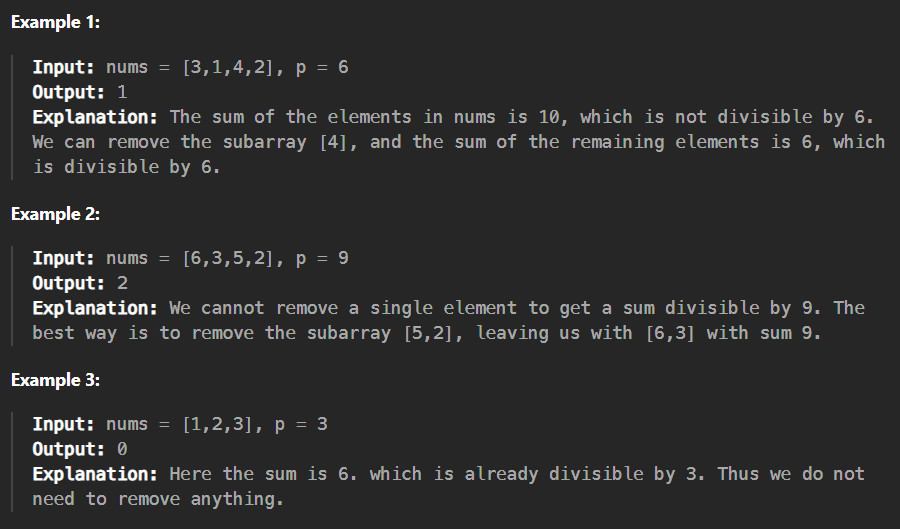
题目概述
Given an array of positive integers nums, remove the smallest subarray (possibly empty) such that the sum of the remaining elements is divisible by p. It is not allowed to remove the whole array.
Return the length of the smallest subarray that you need to remove, or -1 if it’s impossible.
A subarray is defined as a contiguous block of elements in the array.
Constraints:
1 <= nums.length <= 10 ^ 51 <= nums[i] <= 10 ^ 91 <= p <= 10 ^ 9
解法:前缀和 + 哈希表
要想解决这个问题,首先我们需要知道移除什么样的子数组可以使原数组剩余部分的和可以被p整除。对原数组求和并取其对p的模(也就是余数)remain,那么满足条件的子数组的和对p取模也应当为remain(当remain = 0时子数组为空)。这样一来,原本的问题就转化成:从给定数组nums中移除一个子数组,该子数组的和对p取模的值为remain,求被移除子数组的最短长度(可以为0),如果不存在这样的子数组则返回-1。
进一步思考计算子数组和的方式。根据题目中给出的nums长度,上限在$10 ^ 5$,如果使用双指针遍历肯定会TLE。更好的做法是用前缀和,计算数组各索引下和的累计值,子数组首尾的累计值做减法即可得到对应区域内的和,当然在这个过程中还需要用一个哈希表来存储各索引下的累计和。下面说说针对这个问题的具体解决办法。
首先,如果remain = 0可以直接返回0,因为当前的数组已经满足整除要求,无需再移除子数组,并且题目允许子数组为空。除此之外的情况则依次遍历数组中的元素,并更新各个索引下的前缀和,这里称之为cur_sum。由于我们想要得到子数组和对p取模的值,那么在哈希表中存储的也应当是各个前缀和对p取模的值,及其对应的索引。结合一个例子来看看:
上方的蓝色数字代表索引,下方的橙色数字代表对应索引下的前缀和。整个数组的和为16,对9取模为7,那么我们需要移除的子数组和对9取模也应当为7。这里相比起直接观察前缀和,替换成其对9取模的值将更加直观:
\[\overset{\color{royalblue}{0}}{\underset{\color{orange}{6}}{6}} \quad \overset{\color{royalblue}{1}}{\underset{\color{orange}{0}}{3}} \quad \overset{\color{royalblue}{2}}{\underset{\color{orange}{5}}{5}} \quad \overset{\color{royalblue}{3}}{\underset{\color{orange}{7}}{2}} \qquad p = 9\]当子数组和对p取模的值为remain时,需要满足以下条件:(prefix_sum[j] % p - prefix_sum[i] % p) % p = remain,j >= i。这里j为子数组末尾的索引,i为子数组头部的前一个索引。实际的求解过程中因为会依次更新对应索引的前缀和,所以prefix_sum[j] % p和remain是已知量,需要根据这两个量寻找符合条件的prefix_sum[i] % p,那么哈希表中就应当存储各个前缀和对p取模的值以及对应的索引,这个思路类似two sum。此外,题目中要求子数组长度最小,所以哈希表中只需存储各个前缀和对p取模的值在数组中对应的最右侧的索引即可,也就是按照遍历顺序覆盖式更新。
代码实现
初始化
1
2
3
4
cur_sum = 0
remain = sum(nums) % p
ans = len(nums)
index_map = {0: -1}
cur_sum用于计算各个索引下的前缀和,remain表示整个数组和对p取模的值,ans答案初始化为最大值——数组的长度。特别需要注意的是哈希表index_map的初始化,需要提前存储子数组从索引0开始的情况。依照之前的计算方式,子数组头部索引的前一个索引设定为-1以便于后续计算;前缀和为0,因为这时对应的是一个空的前缀数组。
不需要移除子数组的情况
1
2
if not remain:
return 0
整个数组的和恰好已经被p整除,无需移除子数组,返回答案为0。
遍历数组
1
2
3
4
5
6
7
for i, num in enumerate(nums):
cur_sum += num
cur_remain = cur_sum % p
target = (cur_remain - remain) % p
if target in index_map:
ans = min(ans, i - index_map[target])
index_map[cur_remain] = i
有几个需要注意的点。
寻找满足条件的子数组。已知量为
cur_remain和remain,分别是当前前缀和对p取模的值和整个数组和对p取模的值。根据之前的结论,需要判断哈希表中是否存在满足条件的target(这个target就是之前存储的各个子数组和对p取模的值),使得其与cur_remain做差后得到的子数组和对p取模的值等于remain。Python中进行取余数运算时,余数的符号与除数相同,所以无论做差值得正负都可以得到正确的余数。更新哈希表的时机。哈希表中键值对的更新应当在寻找完
target之后,否则有可能会将之前的有效信息覆盖掉,从而导致计算出错误的结果。
返回结果
1
return -1 if ans == len(nums) else ans
当ans = len(nums)时有两种情况,第一种是没有满足条件的子数组存在,第二种则是需要移除整个数组,但这个操作在题目中不被允许,因此这时返回答案-1;反之则返回计算出的对应ans值。
完整代码
完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
def minSubarray(self, nums: List[int], p: int) -> int:
cur_sum = 0
remain = sum(nums) % p
ans = len(nums)
index_map = {0: -1}
if not remain:
return 0
for i, num in enumerate(nums):
cur_sum += num
cur_remain = cur_sum % p
target = (cur_remain - remain) % p
if target in index_map:
ans = min(ans, i - index_map[target])
index_map[cur_remain] = i
return -1 if ans == len(nums) else ans
结果顺利通过。
Time complexity: $O(n)$
Space complexity: $O(p)$