题目概述
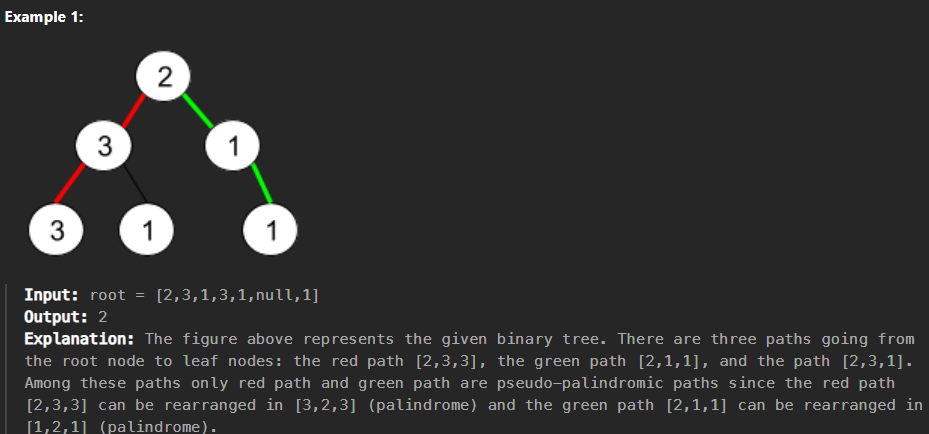
Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.
Return the number of pseudo-palindromic paths going from the root node to leaf nodes.
Constraints:
- The number of nodes in the tree is in the range
[1, 10 ^ 5]. 1 <= Node.val <= 9
思路 & 代码实现
首先分析一下题目。想要解决这个问题可以分两步走:
- 遍历二叉树, 找出其中所有以根节点为起点,叶节点为终点的路径,并记录路径中每个值的个数
- 根据记录的路径信息判断该路径是否是伪回文路径,并计数
尝试1:DFS + 数组
首先,为了获取二叉树中所有满足条件的路径,需要对其中的节点进行遍历。这里采用 前序遍历(Preorder Traversal) 会比较符合思维习惯,也即当访问到某一节点时,就将这个节点中存储的值记录到路径中,然后再依次遍历该节点的左子节点和右子节点。于此同时为了记录每一条路径的信息,需要一个数组用来存储已访问的节点的值。至此,我们可以定义以下函数:
1
2
def dfs(node, path):
path.append(node.val)
其中,node对应的是当前访问的节点;path对应的是一个数组,其中存储了路径行进至当前节点时所包含的所有的值。接下来要做的是判断路径何时行进至终点,也即叶节点,以及完善前序遍历的逻辑。
根据叶节点的定义,它是一个没有子节点的节点。所以只需在函数中添加如下判断:
1
2
3
4
5
def dfs(node, path):
path.append(node.val)
if not node.left and not node.right:
# 判断路径是否是伪回文路径,并计数
return
接下来完善整个遍历部分的逻辑。这里明确一点,此文中dfs这个函数在遍历二叉树时遵循访问到的节点一定存在这个原则,也就是说在函数进入下一次递归之前就已经对子节点的存在性进行了判定。此外,还有一个很重要的点是,当某一条路径探索完成后结束递归并返回上一层时需要将当前路径节点的值弹出,以确保每条路径的信息互不干扰。最后完整的代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
def dfs(node, path):
path.append(node.val)
if not node.left and not node.right:
# 判断路径是否是伪回文路径,并计数
return
if node.left:
dfs(node.left, path)
path.pop()
if node.right:
dfs(node.right, path)
path.pop()
至此,遍历部分完成。接下来探讨如何判断一条路径是否是伪回文路径。
根据题目定义,对该条路径中存在的所有整数值进行排列,只要存在一组排列的结果为回文数(回文数定义)则该路径为伪回文路径。如果我们按照这个定义去进行判断的话需要对数组进行全排列,时间复杂度过高,故而不可取。为了提高效率,让我们来看看一个回文数具有怎样的特征。首先按照数的长度,我们可以把它们分为奇数长度与偶数长度两类:
- 奇数长度: 181, 9, 10001
- 偶数长度: 22, 9988, 10100101
观察后可以发现,偶数长度下每一种数字都必然存在偶数个,否则会有一种数字落单而导致无法形成回文数;而奇数长度下必然有且只有一种数字存在奇数个,负责也会导致有数字落单。将这个结论再进行一次归纳的话,可以得到:
当一个数为回文数时,出现次数为奇数的数字种类至多不会超过一个。
所以,判断一个数是否为回文数的话,只需依照这个结论即可。python中可以通过以下方法实现:
1
2
3
4
5
6
7
8
9
from collections import Counter # leetcode中无需此语句
def isPseudoPalindromic(path):
counter = Counter(path)
odd, even = 0, 0
for n in counter.values():
odd += n % 2
even += (not n % 2)
return odd <= 1
odd, even分别为该路径中出现次数为奇数、偶数的数字种类数。
最后,我们将两部分内容合并,并将答案记录在变量self.ans中:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
def pseudoPalindromicPaths (self, root: Optional[TreeNode]) -> int:
self.ans = 0
def isPseudoPalindromic(path):
counter = Counter(path)
odd, even = 0, 0
for n in counter.values():
odd += n % 2
even += (not n % 2)
return odd <= 1
def dfs(node, path):
path.append(node.val)
if not node.left and not node.right:
self.ans += isPseudoPalindromic(path)
return
if node.left:
dfs(node.left, path)
path.pop()
if node.right:
dfs(node.right, path)
path.pop()
dfs(root, [])
return self.ans
将这个做法提交,得到的结果:超出时间限制!
错误分析
根据先前尝试的结果,这个解法显然还可以在时间上进行优化。由于之前的解法在步骤上分为了两部分,所以我们可以对每一个步骤进行时间复杂度上的分析。
- 遍历部分: 在路径探索时采用前序遍历,故而对于整个树来说每个节点至多被访问一次,因此时间复杂度为 $O(n)$
- 判断伪回文路径部分: 使用了
Counter计数, 因此时间复杂度为 $O(n)$
由于判断伪回文路径函数在每次路径探索终止时都会被调用,因此整个算法的时间复杂度为 $O(n ^ 2)$
考虑到按照题意完成所有的路径探索是得出正确答案的必要条件,所以对于时间上的优化只能在 判断伪回文路径 部分完成。
尝试2:DFS + 位运算
再次研究题目给出的条件后发现,因为组成一个整数的数字种类只能是1~9中的一种,因此相较于数组,一个初始值为0的二进制数是更优的信息存储方式。举个例子,如果在节点处取出的值是4,那么我们就对这个二进制数的第四位进行翻转操作:
\[\begin{aligned} 0000 \rightarrow \textcolor{red}{1}000 \end{aligned}\]这里的 0 和 1 代表每一位对应的数字出现了 偶数次 或者 奇数次 。
根据节点值翻转对应位数的操作可以用如下方法实现:
1
2
def dfs(node, path):
path ^= 1 << (node.val - 1)
一个二进制数的第 $n$ 位对应的是 $2 ^ {n - 1}$ ,而这里 $n$ 的值对应的就是此题中的 node.val ,故采用左移实现幂运算。这样一来我们可以仅通过 维护一个二进制数来记录路径中各个数字出现了奇数次还是偶数次 。
接下来探讨如何利用这个二进制数判断路径是否为伪回文路径。
根据先前得出的结论:当一个数为回文数时,出现次数为奇数的数字种类至多不会超过一个, 可以得出代表符合条件路径的二进制数中 至多只会有一位是1 。这时候如果利用 统计一个二进制整数中1的个数 这个问题中用到的技巧:
1
path &= path - 1
便可以将原本二进制数中最右侧的1移除。对于符合伪回文路径判断条件的二进制数来说,分为两种情况:
- 该二进制数中只有一位是1,那么利用上面提到的方法可以将唯一的1移除,令操作后的值为0
该二进制数没有任何一位是1,也即其值为0。那么上述操作就变为:
1
path = 0 & -1
负数的二进制表示方式可以参考 此处 。此时-1对应的二进制表示为
11111111, 所以在和0进行按位与操作后得到的结果也为0
综上,使用这个方法后符合条件的二进制数为变为0,反之则不会。因此我们可以采用以下方式进行伪回文路径的判定:
1
2
def isPseudoPalindromic(path):
return not path & (path - 1)
结合以上方法,最终可得:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
def pseudoPalindromicPaths (self, root: Optional[TreeNode]) -> int:
self.ans = 0
def isPseudoPalindromic(path):
return not path & (path - 1)
def dfs(node, path):
path ^= 1 << (node.val - 1)
if not node.left and not node.right:
self.ans += isPseudoPalindromic(path)
return
if node.left:
dfs(node.left, path)
if node.right:
dfs(node.right, path)
dfs(root, 0)
return self.ans
Time complexity: O(n)
Space complexity: O(h) (此处 $h$ 代表二叉树的高度)
结果顺利通过。